Interleaving String
If you are interested about this problem, please visit this link for more information about the problem description.
This post expresses a way of thinking by using dynamic programming technique.
Understand the problem
You are given three string arguments, say s1, s2 and s3 where you are going to check whether if s1 and s2 can be
formed into s3 in an interleaving way.
An interleaving way can be visualized in this image
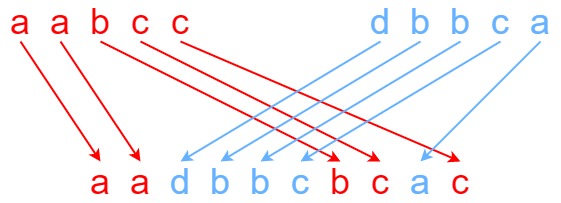
Work through problem
When it comes to Dynamic programming, we can think of it as a table where the solutions and subsolutions are built or calculated based on the previous solution.
A table
Before we start, I want to use this one as an example:
**Input**: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac" */
| ”“(0) | d(1) | b(2) | b(3) | c(4) | a(5) | |
|---|---|---|---|---|---|---|
| ”“(0) | T | F | F | F | F | F |
| a(1) | T | F | F | F | F | F |
| a(2) | T | T | T | T | T | F |
| b(3) | F | T | T | F | T | F |
| c(4) | F | F | T | T | T | T |
| c(5) | F | F | F | T | F | T |
The row represents for string s2 and the column represents for string s1, and the numbers beside them are indices.
The string s3 as follow:
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Char | a | a | d | b | b | c | b | c | a | c |
The code
if (i == 0 && j == 0) { // Empty String
dp[i][j] = true;
} else if (i == 0) { // First row
dp[i][j] = dp[i][j-1] && s2[j-1] == s3[i+j-1];
} else if (j == 0) { // First col
dp[i][j] = dp[i-1][j] && s1[i-1] == s3[i+j-1];
} else {
dp[i][j] = (dp[i-1][j] && s1[i-1]==s3[i+j-1]) || (dp[i][j-1] && s2[j-1] == s3[i+j-1]);
}
Conclusion
By studying the condition above, you can understand the table.
The idea is that, if you see the row dp[i-1][j] is true, so you know this character
can be formed to string s3, but that is not enough, we have to check the string s2 that is the column too,
that is why we see condition if dp[i-1][j] is true, ok, let check the s2[j - 1] if it can also be formed to s3.
It’s hard to understand by reading, I know, but believe me, you will truly understand it when you have a pencil and a paper, start to with an empty table, studying the idea of dynamic programming, start filling the table based on the condition.