N-Queens

Description

You may have clicked on the link above and read the description of the problem but I will simplify it in here: You’re given an integer n represents n x n chessboard such that no two queens attack each other.

Let’s look at this beautiful (I’m kidding) picture that I draw:

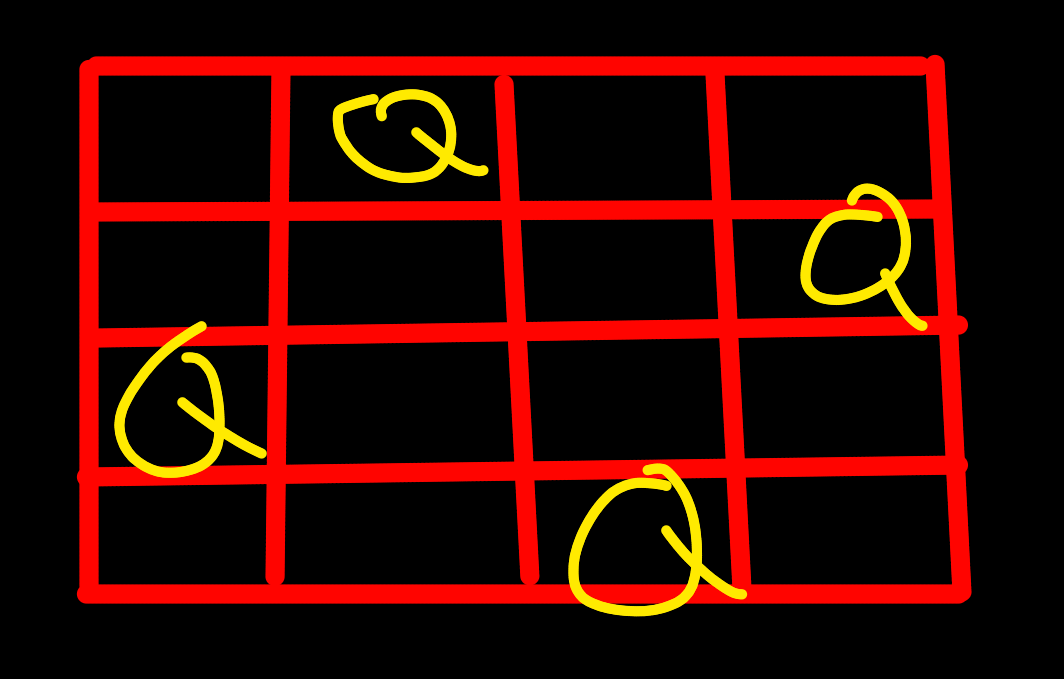
demo1

So basically, you put the n queens on the n x n chessboard so that there is no two queens attack each other.

Ideas

There may many ideas that come to mind, but one must notice is that this problem is very associated with backtracking. We have to make the choices that is how to put queens in the right place, and if we put them in the wrong place, then we have to go back and explore other places that we could put.

After a certain amount of time, we meet the base case (condition), which is we know that there is no need to travel on the chessboard because all the queens have to sit in the right places. There you go.

So how would we do that? The idea is very simple:

Create a chessboard n x n

    let mut answers: Vec<Vec<String>> = Vec::new();
    let mut board = vec![vec!['.'; n as usize]; n as usize]; // Init board

Check if the current board[row][col] is safe? if it is, mark board[row][col] as ‘Q’

        for col in 0..n {
            if is_safe(&board, row, col, n) {
                board[row][col] = 'Q';
                solve(board, answers, row + 1, n); // Move to the next row
                board[row][col] = '.'; // prunching
            }
        }

Notice the line here: ` solve(board, answers, row + 1, n); // Move to the next row`

We have to go back to explore the next row, but you know that, suppose we put the queen in here:

demo1

Then there are plenty of possible options we could make:

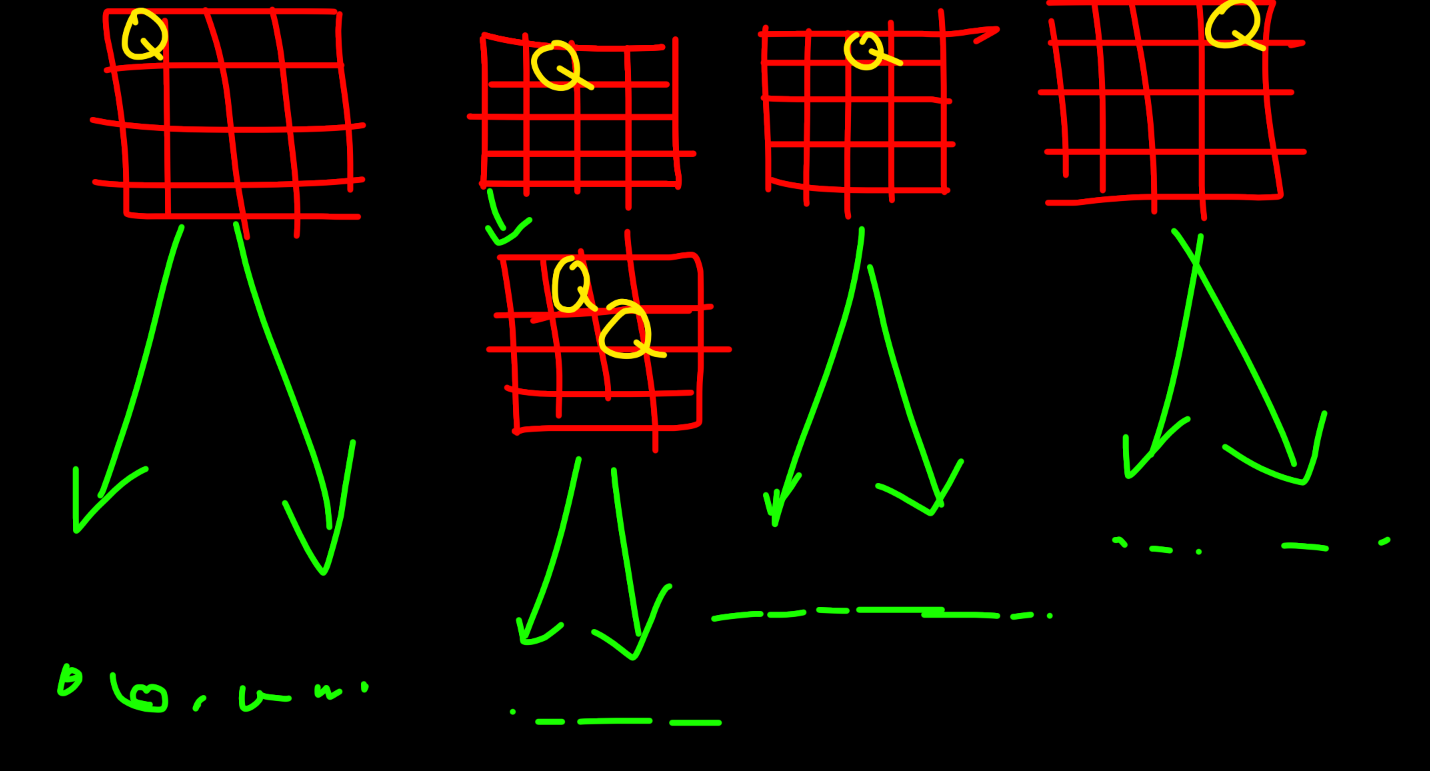
demo1

We make the choices, repeat, go back and then make the choice, go back again until we make the whole right choice. Isn’t it interesting?

Entire (Doesn’t matter) code. I think ideas is more matter than the code, because the code is just how we express our ideas.

pub fn solve_n_queens(n: i32) -> Vec<Vec<String>> {
    let mut answers: Vec<Vec<String>> = Vec::new();
    let mut board = vec![vec!['.'; n as usize]; n as usize]; // Init board

    fn is_safe(board: &Vec<Vec<char>>, row: usize, col: usize, n: usize) -> bool {
        // Check for current column
        for i in 0..row {
            if board[i][col] == 'Q' {
                return false;
            }
        }

        let mut i = row as i32;
        let mut j = col as i32;
        while i >= 0 && j >= 0 {
            if board[i as usize][j as usize] == 'Q' {
                return false;
            }
            i -= 1;
            j -= 1;
        }

        i = row as i32;
        j = col as i32;
        while i >= 0 && j < n as i32 {
            if board[i as usize][j as usize] == 'Q' {
                return false;
            }
            i -= 1;
            j += 1;
        }
        true
    }
    fn solve(
        board: &mut Vec<Vec<char>>,
        answers: &mut Vec<Vec<String>>,
        row: usize,
        n: usize
    ) {

        if row == n {
            let mut ans: Vec<String> = Vec::with_capacity(n);
            for i in 0..n {
                ans.push(board[i].iter().collect());
            }
            answers.push(ans);
            return;
        }
        for col in 0..n {
            if is_safe(&board, row, col, n) {
                board[row][col] = 'Q';
                solve(board, answers, row + 1, n);
                board[row][col] = '.'; // prunching
            }
        }
    }

    solve(&mut board, &mut answers, 0, n as usize);
    answers
}

Remember, it’s not that complicated once we know backtracking is on our side.